Trees Made to Order
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6290 | Accepted: 3619 |
Description
We can number binary trees using the following scheme:
The empty tree is numbered 0.
The single-node tree is numbered 1.
All binary trees having m nodes have numbers less than all those having m+1 nodes.
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either Left subtrees numbered higher than L, or A left subtree = L and a right subtree numbered higher than R.The first 10 binary trees and tree number 20 in this sequence are shown below: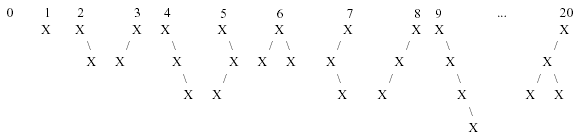
Your job for this problem is to output a binary tree when given its order number.
The empty tree is numbered 0.
The single-node tree is numbered 1.
All binary trees having m nodes have numbers less than all those having m+1 nodes.
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either Left subtrees numbered higher than L, or A left subtree = L and a right subtree numbered higher than R.The first 10 binary trees and tree number 20 in this sequence are shown below:
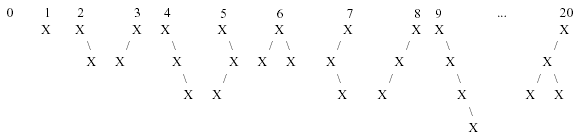
Your job for this problem is to output a binary tree when given its order number.
Input
Input consists of multiple problem instances. Each instance consists of a single integer n, where 1 <= n <= 500,000,000. A value of n = 0 terminates input. (Note that this means you will never have to output the empty tree.)
Output
For each problem instance, you should output one line containing the tree corresponding to the order number for that instance. To print out the tree, use the following scheme:
A tree with no children should be output as X.
A tree with left and right subtrees L and R should be output as (L’)X(R’), where L’ and R’ are the representations of L and R.
If L is empty, just output X(R’).
If R is empty, just output (L’)X.
Sample Input
1 20 31117532 0
Sample Output
X ((X)X(X))X (X(X(((X(X))X(X))X(X))))X(((X((X)X((X)X)))X)X)
Source
main里面先算指定节点个数有多少个二叉树(类斐波那契数列),再算总共排到一个数字是多少个二叉树。
之后给定一个树,先看多少个节点,然后看是否是单独左子树,右子树,如果都不是看左右分别有多少。cn为当前子树节点个数,计算出c为当前左右子树个数下的第几个,k为左子树节点个数,cn-k-1为右子树节点个数。
慢慢调就出来了,然而调的也太慢了吧。。。。。
#include <iostream>
#include <algorithm>
#include <functional>
#include <stdio.h>
#include <string>
#include <vector>
#include <functional>
#include <string>
#include <map>
using namespace std;
#define MAXN 23
long i = 500000000;
long num[MAXN];
long cml[MAXN];
void get(long n){
if(n==1){
// char *ret = new char[2];
// strcmp(ret,"X");
printf("X");
return;
}
long cn = 0;
for(long i=0;i<MAXN;i++){
if(cml[i]>=n)
{
cn = i;
break;
}
}
if(n<=cml[cn-1]+num[cn-1]){
// R only
char *ret = new char[100];
long nn = n-cml[cn-1]+cml[cn-2];
printf("X(");
get(nn);
// printf("%s",get(nn));
printf(")");
return;
}
else if(n>cml[cn]-num[cn-1]){
//L only
long nn = n-(cml[cn]-num[cn-1])+cml[cn-2];
printf("(");
get(nn);
// printf("%s",get(nn));
printf(")X");
return;
}
else{
long c = n,k=1;
c-=cml[cn-1];
c-=num[cn-1];
long L=0,R=0;
while(true){
if(c>num[k]*num[cn-k-1]){//?? >=?
c-=num[k]*num[cn-k-1];
k++;
}
else{
long Rno = num[cn-1-k];
c=c-1;
if(k==1){
L=1;
}else{
L = c/Rno;
L+=cml[k-1]+1;
}
if(cn-1-k==1){
R=1;
}else{
R = c%Rno;
R+=cml[cn-1-k-1]+1;
}
break;
}
}
// for()
printf("(");
// printf("%s",get(L));
get(L);
printf(")X(");
get(R);
// printf("%s",get(R));
printf(")");
return;
}
}
int main(){
num[0]=1;
num[1] = 1;
num[2] = 2;
long res = 0;
for(long i=3;i<MAXN;i++){
res = 0;
for(long j=0;j<=i;j++){
res+=num[j]*num[i-j-1];
}
// if((i%2)==0){
// for(long j=0;j<=i;j++){
// res+=num[j]*num[i-j];
// }
// }else{
// for(long j=0;j<i;j++){
// if(j==((i-1)/2)){
// res+=num[j];
// continue;
// }
// res+=num[j]*num[i-j-1];
// }
// }
num[i] = res;
}
cml[0] = 0;
for(long i=1;i<MAXN;i++){
cml[i] = cml[i-1]+num[i];
// cout<<cml[i]<<endl;
}
long i = -1;
while(scanf("%ld",&i)){
if(i==0){
break;
}
get(i);
printf("\n");
}
return 0;
}
